Cayley's formula

In mathematics, Cayley's formula is a result in graph theory named after Arthur Cayley. It states that for any positive integer n, the number of trees on n labeled vertices is .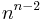

The formula equivalently counts the number of spanning trees of a complete graph with labeled vertices.

Proof

Many remarkable proofs of Cayley's tree formula are known. One classical proof of the formula uses Kirchhoff's matrix tree theorem. Prüfer sequences yield a bijective proof of Cayley's formula. Another bijective proof, by André Joyal, finds a one-to-one transformation between n-node trees with two distinguished nodes and maximal directed pseudoforests. A proof by double counting, due to Jim Pitman, can be seen at Double counting (proof technique)#Counting trees.

History

The formula was first discovered by Carl Wilhelm Borchardt in 1860, and proved via a determinant. In a short 1889 note, Cayley extended the formula in several directions, by taking into account the degrees of the vertices. Although he referred to Borchardt's original paper, the name "Cayley's formula" became standard in the field.

References

• Aigner, Martin; Ziegler, Günter M. (1998). Proofs from THE BOOK. Springer-Verlag. pp. 141–146. .
• Borchardt, C.W. (1860). "Über eine Interpolationsformel für eine Art Symmetrischer Functionen und über Deren Anwendung". Math. Abh. der Akademie der Wissenschaften zu Berlin: 1–20. 
• A. Cayley (1889). "A theorem on trees". Quart. J. Math 23: 376–378. http://books.google.com/?id=M7c4AAAAIAAJ&pg=PA26. 
• Shukla, Alok (2009). "A short proof of Cayley's Tree Formula". arXiv:0908.2324 [math.CO]. .